多源最短路径算法–Floyd算法
Floyd算法是为了求出每一对顶点之间的最短路径
它使用了动态规划的思想,将问题的求解分为了多个阶段
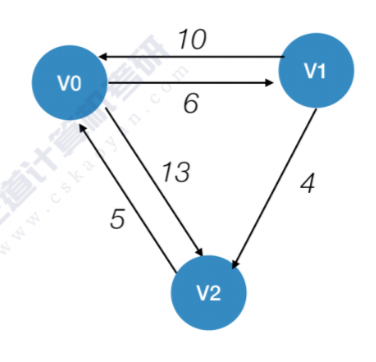
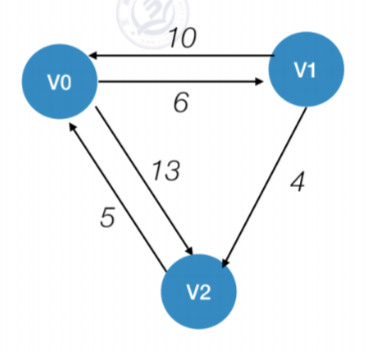
先来个例子,这是个有向图
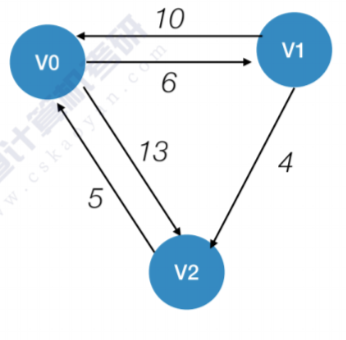
Floyd算法的运行需要两个矩阵
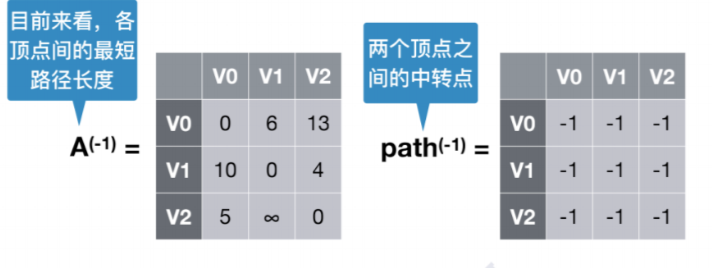
最短路径矩阵
从当前这个状态看各顶点间的最短路径长度
例如初始状态
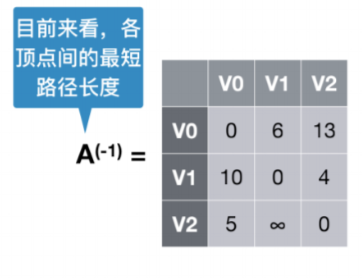
可以看出这是该有向图的邻接矩阵
顶点之间中转点矩阵
初始状态都没有中转点
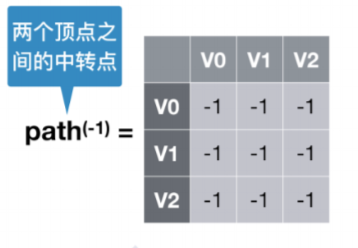
引入中转点
A(k-1)代表引入顶点k-1时,各个顶点的最短路径状态
path(k-1)代表引入顶点k-1后,各个顶点的最短路径需要经过哪个结点

判断顶点i到顶点j,如果经过顶点k,是否会更短?
如果更短,改变A(k-1)数组中i结点到j结点的最短路径,同时更改path(k)数组,表明经过顶点k,顶点i到顶点j路径更短
- 允许在V0中转,计算出当前的最短路径
顶点2到顶点1
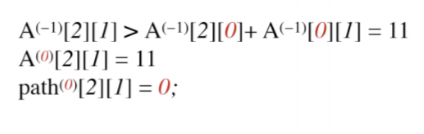
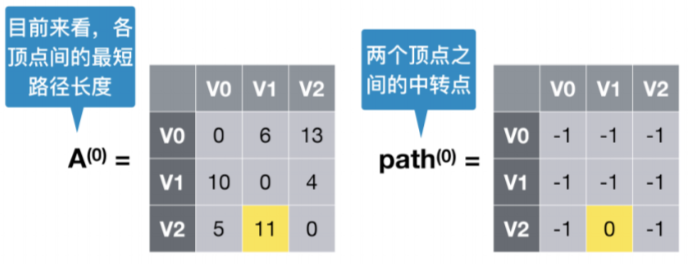
可以看到原来顶点2到顶点1是没有路径的,通过V0之后,最短路径变为11,那么更新A(0)数组,A(0)数组代表引入V0之后个顶点之间的最短路径,同是更新path(0)数组,代表V2到V1经过了V0

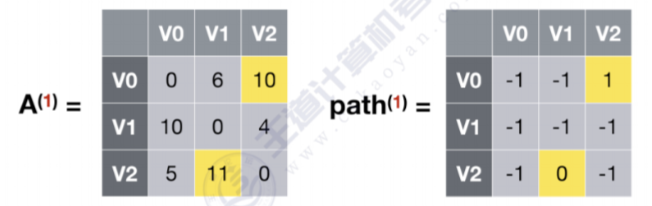
- 允许在V0,V1中转,计算出当前的最短路径
顶点0到顶点2
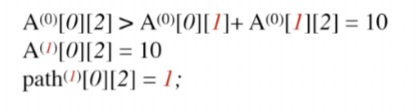
可以看到原来顶点0到顶点2的距离是13,通过V1之后,最短路径变为10,那么更新A(1)数组,A(1)数组代表引入V1之后个顶点之间的最短路径,同是更新path(1)数组,代表V0到V2经过了V1
- 允许在V0,V1,V2中转,计算出当前的最短路径
顶点1到顶点0
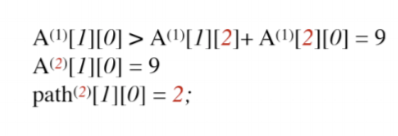

可以看到原来顶点1到顶点0的距离是10,通过V1之后,最短路径变为9,那么更新A(2)数组,A(2)数组代表引入V2之后个顶点之间的最短路径,同是更新path(2)数组,代表V1到V0经过了V2
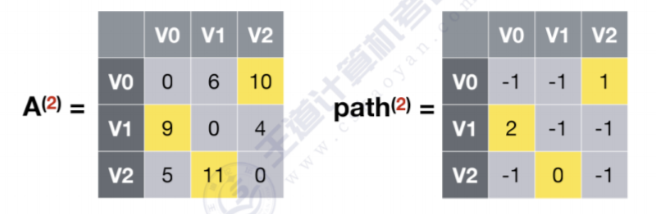
- 最终结果

- 核心代码

再看一个新的例子
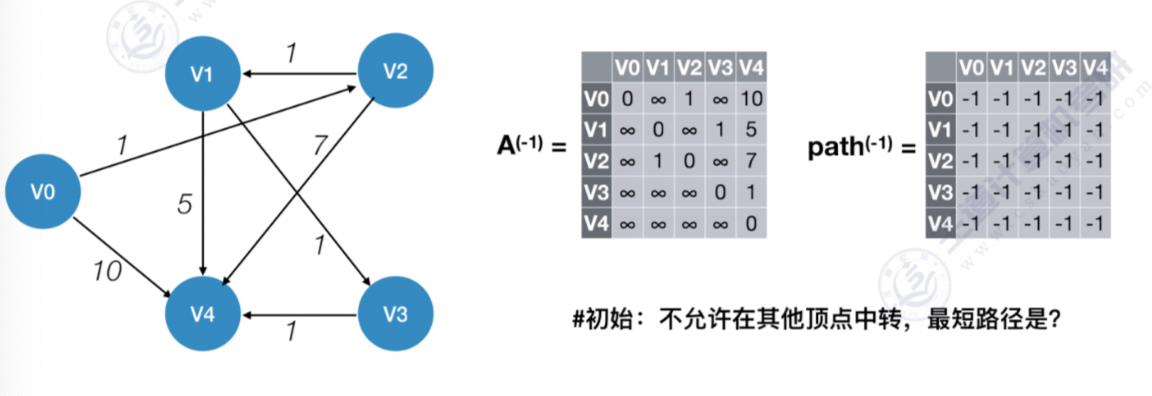
- 允许在V0中转,k=0

所有结点之间都不能通过V0获得更短的路径,故不更新A(0)数组和path(0)数组
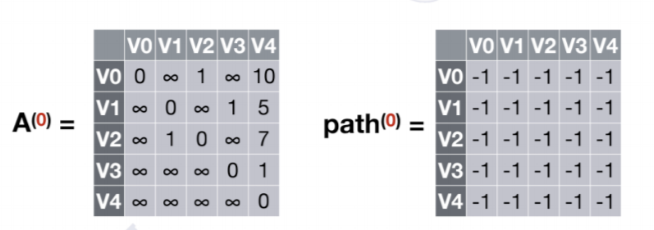
- 允许在V0,V1中转,k=1


V2到V3和V2到V4经过V0,V1中转有更短的路径,故更新A(1)数组和path(1)数组
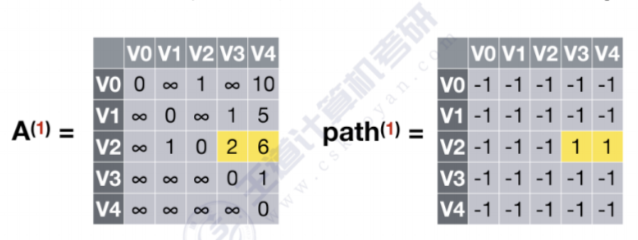
- 允许在V0,V1,V2中转,k=2


V0到V1,V0到V3,V0到V4经过V0,V1,V2中转有更短的路径,故更新A(2)数组和path(2)数组
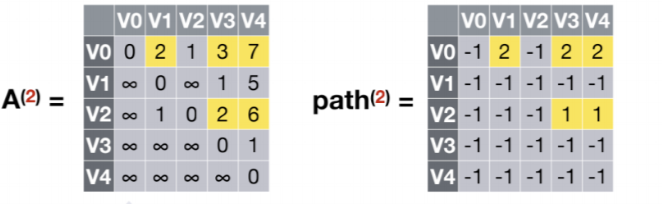
- 允许在V0,V1,V2,V3中转,k=3


V0到V4,V1到V4,V2到V4经过V0,V1,V2,V3中转有更短的路径,故更新A(3)数组和path(3)数组
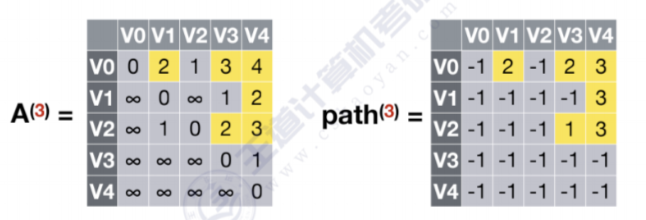
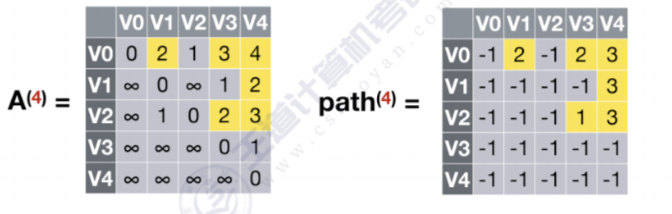
- 允许在V0,V1,V2,V3,V4中转,k=4

所有结点之间都不能通过V4获得更短的路径,故不更新A(4)数组和path(4)数组
注意
- Floyd算法不能解决带有“负权回路”的图,这种图可能没有最短路径




