学习周报：文献阅读+Fluent案例+Fluent相关算法学习

目录

摘要

Abstract

文献阅读：求解正逆运动波问题的物理信息神经网络

文献摘要

讨论|结论

理论基础

KWM（运动波动方程）

Hard constraint （硬约束方式）

具有重新分布的搭配点的PINN

具有停止梯度的分数阶方程

实验设置

正运动学波问题

稳定降雨案例

不稳定降雨情况

逆运动波问题

Fluent实例：分流管道中的流动分析

几何建模

网格划分

求解器设置

结果展示

理论学习部分

总结

摘要

在本周中，通过阅读文献，了解PINN的新形式RCP-PINN，文章中使用传统PINN和RCP-PINN对于3个问题的结果进行对比试验，包括两个正问题和一个逆问题，证明了RCP-PINN在实际运用中的可行性，并阐述了优缺点。在Fluent中，选用内分流管道中的流动分析，进行几何划分和设置求解。理论学习方面，对有luent算法基本知识进行了学习。

Abstract

In this week, I read the literature to learn about the new form of PIN, RCP-PINN, and used the traditional PIN and RCP-PINN to compare the results of 3 questions, including two positive questions and one inverse problem, to prove the feasibility of RCP-PINN in practical application, and to explain the advantages and disadvantages. In Fluent, I use the flow analysis in the inner shunt pipe to do the geometry and setup the solution. In terms of theoretical learning, I learned the basic knowledge of luent algorithms.

文献阅读：求解正逆运动波问题的物理信息神经网络

Physics-informed neural network for solution of forward and inverse kinematic wave problems

文献摘要

一维运动波模型(KWM)广泛应用于地表水和水质水文，以及长公路上的交通运动建模，由于其涉及一个一阶非线性偏微分方程，该方程可以用数值方法求解真实的几何表示、输入、初始条件和边界条件。

文章从此角度，提出了一种利用神经网络结构求解偏微分方程的方法，即使用PINN应用于正、逆问题的一维非线性KWM求解。文章中的创新点如下：

1. 为了提高精度和收敛性，抑制陡坡锋面的杂散振荡，采用了一种改进的PINN算法——重分布配点技术（RCP-PINN）。
2. 为了处理非线性平流项的分数阶，提出了一种停止梯度技术。

为了验证这一点，文章对正向问题进行了定常、非定常坡面流和无侧流明渠流的KWM分析。对于反问题，正确计算了未知的Manning系数，验证了所提算法辨识KWM参数的能力。

优劣势如下：

1. 与原有的PINN相比，它没有增加额外的计算成本；
2. 与PINN相比，RCP-PINN预测结果更准确，训练过程中的损失收敛过程更快、更稳定。与经典的SA算法相比，原PINN算法及其修正算法的计算次数要少得多。
3. 在没有任何指导的情况下，保留点的数量可能会随着具体问题的变化而变化，这是有限制的。这使得这种方法在一定程度上还依赖于经验和实践。

讨论|结论

KW问题可以分为正解和逆解两类。在正向问题中，已知系统几何形状、输入、初始条件和边界条件，并确定系统输出。例如：在给定初始流深和上游条件下，求解整个时空范围内的水深和流量分布，恢复水力流程图，预测洪波。针对不同的流入和流域条件，已经推导出了各种KWM的解析解、半解析解和近似解。

在反问题中，KW方程的参数是未知的，应该通过给定的初始条件和边界条件以及观测来确定。KW方程中的参数为曼宁系数和平面斜率。坡度可以通过简单的测量直接得到，因此不需要确定。当曼宁系数未知时，其估算对于估算行程时间和排水设计具有实际意义。

目前方法存在的局限在于：

1. 在求解正演问题时，这些方法对具有光滑解的问题给出了准确的解，换而言之，在不具有光滑解时，可能在陡锋(激波)处出现数值扩散和/或伪振荡。
2. 对于解逆问题，这些方法并不总是令人满意的。

故引出使用PINN来进行求解KW问题的方式，pinn的优势是双重的:

(1)首先，它依赖于自动微分技术，该技术可以轻松实现训练过程，近似解的导数，并在整个解域中获得连续解。

(2)其次，同一个框架既可以用来解决正向问题，也可以用来解决逆向问题，而且实现起来很简单。

但是以往的PINN方式依赖于训练点的数量，点分布的选项包括uniform, LHS, Sobol和其他策略，Sobol策略和LHS一样，也是一种分层抽样，采样域是均匀划分的，每个部分只有一个采样点。与LHS相比，Sobel策略要求采样点的个数为2n(n∈n)。

每种策略的目标都是在整个域内实现或多或少的均匀分布，而不是结合实际问题，而是关注全局属性的泛化。然而，由于具体问题的解空间和性质不同，上述点分布策略很少能获得最优分布和最佳训练效果。

由于初始点和边界点很好地受到其他技术的约束，例如硬约束，。期望的目标是在不增加计算成本(包括空间成本和时间成本)的情况下，通过尽可能优化搭配点的分布来提高原算法的性能。空间成本包括总点数(num_total)和神经网络的大小，时间成本主要是训练epoch (num_epoch)，通常以训练epoch的个数作为衡量标准。

在原来的PINN中，不可能计算出每一个KWM案例的训练损失，发现导致这个缺陷的原因有两个：

1. 在神经网络中，计算出的分数项对象不应小于零，但在实际训练过程中，目标函数h可能具有负训练值。
2. 自动微分技术在反向传播过程中会使分数项出现在分母中。当某些点的水高接近于零时，分数项变得非常大。这就导致当神经网络的参数更新时，它们会超出计算机的数字范围，从而无法计算。文章将采用停止梯度法求解。

如何在兼顾计算成本和精确度的情况下进行求解各种正逆问题，提出了一种配置点重新分布的改进PINN，称为RCP PINN。本文采用Manning方程，上游边界条件为Dirichlet型，下游边界为Neumann型。将其应用于4个KWM正、逆问题，并将RCP-PINN结果与传统方法得到的解析解和参考解进行比较。验证了RCP-PINN算法相对于PINN算法的优越性。

理论基础

KWM（运动波动方程）

运动波动方程是动力波动方程的简化形式，由以下连续性和动量方程组成:

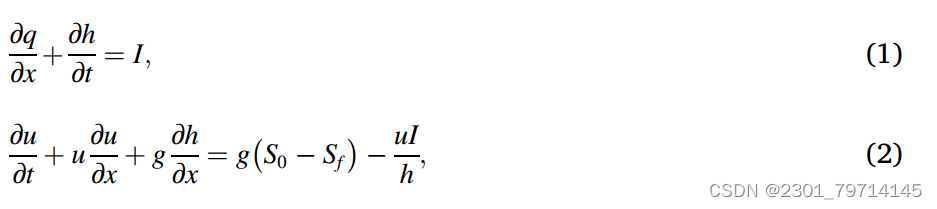
式中，q为单位宽度水量，h为水深，I为侧向入水量，u为水流速度，g为重力加速度，S0为河床斜率，Sf为摩擦斜率。

在（2）式中，局部加速度项(∂u/∂t)、对流加速度项(u×∂u/∂x)、压力梯度项(g×∂h/∂x)和侧向流入力项(uI /h)可以视为次要项，因此可以忽略。因此，摩擦力和重力处于平衡状态，简化后的动量方程为：

Manning和Chezy的方程表示经验放电方程。参照完全湍流时流量与深度的关系，可表示为:

其中nm为Manning系数，Cz为Chezy系数。由简化的动量方程和Manning /Chezy方程推导出通量-浓度方程：

系数：

将连续性方程(1)与通量-浓度方程(6)相结合，可以得到关于水深的非线性方程，有侧向入流的一维坡面流及其初始条件和边界条件的控制方程为:

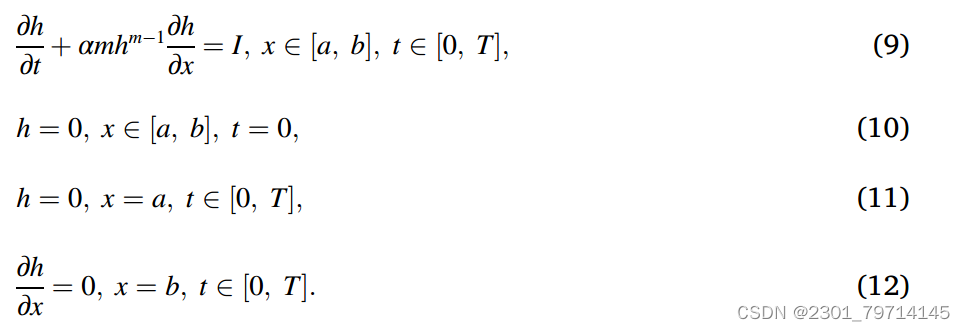
由于运动波动方程是一阶双曲型偏微分方程，它的解只需要一个边界条件。

在运动学中，波浪由上游向下游运动时，不需要式(12)给出的下游边界条件。然而，一些高阶数值格式，如本文所参考的修正全变分递减Lax – Friedrichs (MTVDLF)方法，即使方程是一阶，也需要下游条件。

Hard constraint （硬约束方式）

硬约束和软约束都可以起到约束初始边界条件的作用，但它们在神经网络中的实现机制不同。软约束主要是增加损失项，并通过迭代优化来达到效果。

硬约束通过转换神经网络的输出在特定条件下工作，包括初始、狄利克雷和周期边界条件。

同时，不再需要loss中相应的初始边界项。与软约束相比，硬约束有两个优点:

1. 减少了对计算成本的需求，
2. 应用硬约束时显著改善了训练。

然而，硬约束仍然存在局限性。如果边界条件是诺伊曼或罗宾类型，它将是无效的。它可能会导致某些位置的过拟合，从而降低精度，并且它并不适用于所有问题。一般情况下，根据实际问题，可以同时使用软约束和硬约束。

在实际物理意义上，初始边界条件和上游边界条件都是重要的约束条件，因此在这两个条件下应用硬约束是有效的。它的实现将输出h转换为x × t × h，严格保证了x = 0和t = 0处水深为零。在损失函数中不再需要初始和上游边界损失。

具有重新分布的搭配点的PINN

基本的pINN框架如下所示：

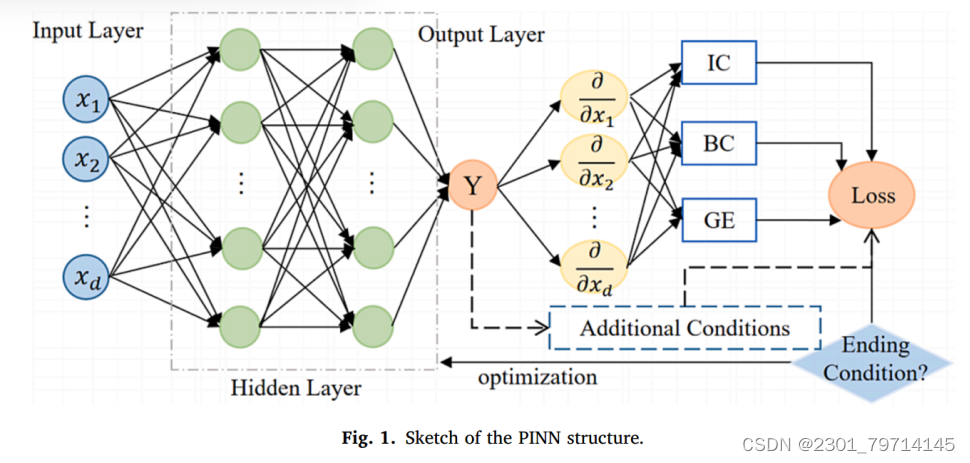
首先，对一定数量的训练epoch应用PINN作为预训练。然后，在时域上收集了测试正交网格点GP0 (n × n)的控制方程损失;进一步绘制粒度更粗的网格G1 (N × N)来划分GP0。基于G1中GP0的网格损耗总和，可以数值化地表示出各个网格的损耗分布。最后，根据损失分布的比例，对整个域的并置点进行重新分布。需要注意的是，本文所考虑的问题都是一维的时空问题，所以配点都是二维的。

在高维问题中，网格的尺寸应相应增大。综上所述，改进算法分为三个阶段，分别为预训练阶段、再分配阶段和正式训练阶段。原PINN算法主要用于预训练阶段和正式训练阶段，其中再分配阶段是本文的重点。

根据控制方程损失和保留的思想，多次动态优化点的分配，而不是只改变一次点的分配。再分配阶段的训练被分成多个训练时段，每个训练时段数相同。在每次训练中，根据当时的训练结果重新分配搭配点，直到达到预设的训练时代。通过每次再分配的结果得到最终解，并在多次分配中选择权重递增的形式。随着训练的进行，神经网络的学习情况会逐渐接近精确解。

假设重新分配的次数为R (R > 1)，具体到第i次分配点，每个粗粒度网格G1的损失和为L[i] j N×N j=1，其和为L[i]，则每个网格中点的损失比例为：

设每个网格中保留的点数为m，则需要重新分配的点数为：

第j个粗网格G1中第i个点分配数的公式为：

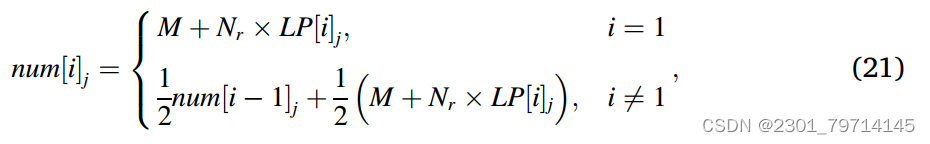
其中num[i] j (1 < i < R, i∈_1)如果不是整数，则将其舍入。

根据上述递推公式，最终得到第j个粗网格G1的动态演化点数为：

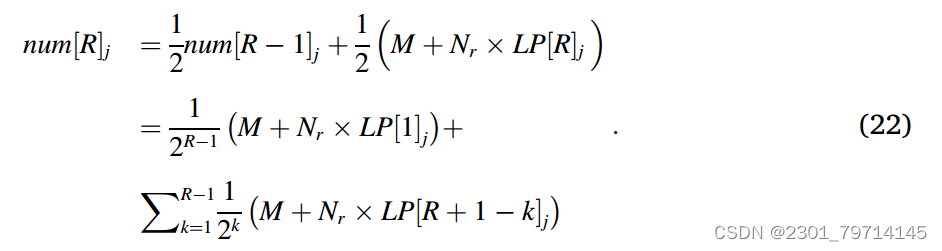
在每个网格中重新确定训练点的个数，并据此使用LHS对训练点进行重新分配。采用上述再分配搭配点技术的PINN在训练过程中实现了搭配点的动态分配，称为RCP-PINN。算法1描述了RCPPINN的详细过程：

上述技术可以应用于使用PINN求解任何偏微分方程。

具有停止梯度的分数阶方程

停止梯度是一种依赖于神经网络的自动推导机制的技术，在训练中利用链式法则对输出结果进行微分，并利用推导结果更新网络参数。停止梯度允许我们有选择地将某些项作为常数处理，而不需要将它们卷入反向推导。这是在分析了KWM的特点后对神经网络进行的调整。

TensorFlow是本文中使用的深度学习框架，其中在tf.gradients()参数中有一个：stop_gradients函数来实现上述想法。

当这种技术应用于一个变量时，它的梯度不会在TensorFlow图中被评估。一项不返回的梯度不会引起神经网络参数更新误差，只是稍微减慢了参数更新速度。在KWM中，如果算法没有传回h23的梯度，则没有项在分母中变为零。这种方法防止了损失中出现过多的数字，使培训工作顺利进行。请注意，停止梯度技术不仅适用于这里考虑的KWM，也适用于其他分数阶方程，当一个值太大而无法在反向传播过程中表示时。

实验设置

正运动学波问题

考虑了空间均匀分布的稳定和非稳定降雨情况。在无侧流问题中，采用变流量作为上游边界条件。所有算例均采用了具有Superbee限制器的MTVDLF方法，为比较和评价提供参考方案，采用TVD方法

稳定降雨案例

稳定入流情况为长度为1000m、坡度为0.01、曼宁系数为0.02的倾斜矩形平面上的坡面流。降雨速率I为30 cm/h，持续时间为1600 s。对于所有x，初始条件为h = 0。

RCP-PINN的参数为:搭配点个数为10000，边界点个数为100。初始点和边界点的选择策略是一致的。训练过程由Adam优化器执行100,000次，学习率为0.001。G1 (10 × 10)的每个网格中保留的搭配点M为50个。在PINN中，除了选择LHS作为搭配点外，进行了相同的设置。MTVDLF的空间步长Δx为10 m，时间步长Δt为0.1 s。

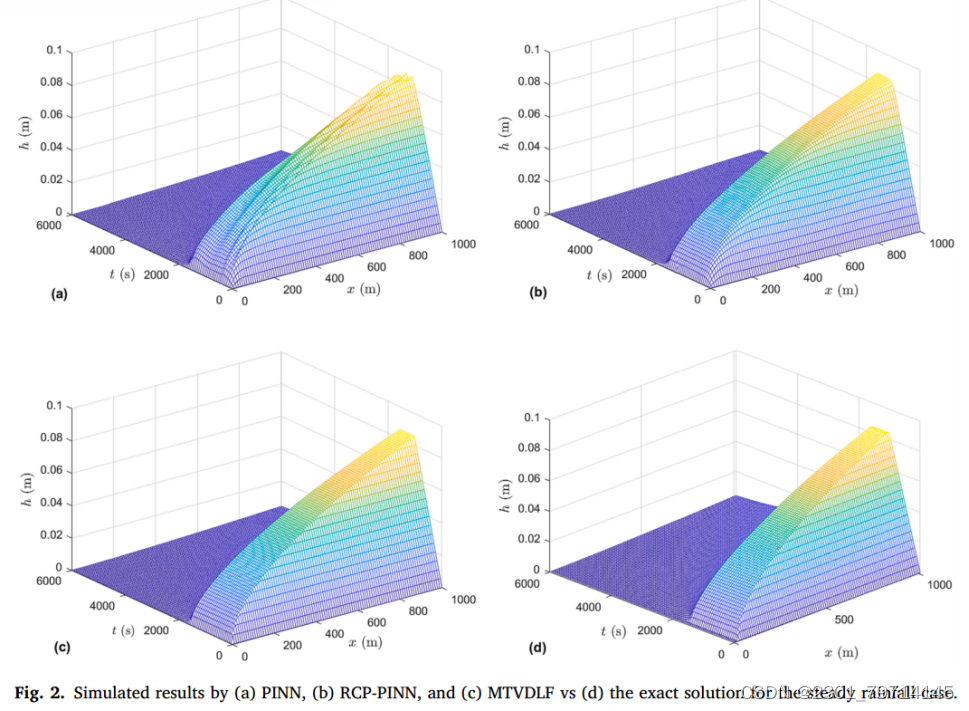
在图2中，将RCP-PINN的结果与PINN、MTVDLF的结果以及解析解在整个时空域上进行比较。可以清楚地观察到，在0 ~ 2000 s的时间范围内，PINN溶液有较大的振荡，而RCP-PINN溶液更接近解析解。误差在时空域的分布对比如图3所示。RCP-PINN的误差主要集中在比原PINN小得多的区域。

由于重复实验中误差之间的巨大差异，虽然PINN获得了准确的结果，但经验发现，在PINN预测中存在一定的不确定性，这归因于模型的不稳定性。

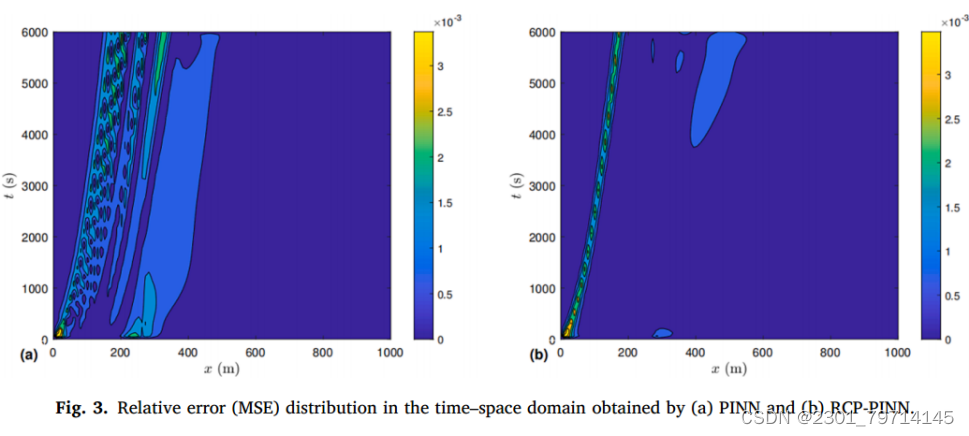
两种方法的搭配点分布如图4所示，以说明两种方法在训练过程采样中的差异。RCP-PINN的点分布由初始分布(图4a)演变为最终分布(图4b)，而图4a中PINN的点分布保持不变。根据RCP-PINN中提出的点选择策略，图4b中的搭配点在控制方程损失较大的位置变得密集，在其他位置变得稀疏。在训练过程中，搭配点的总数保持不变：

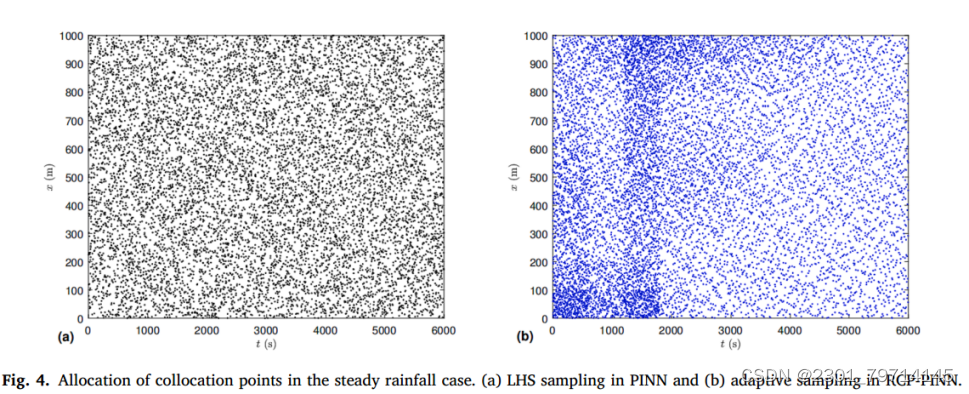
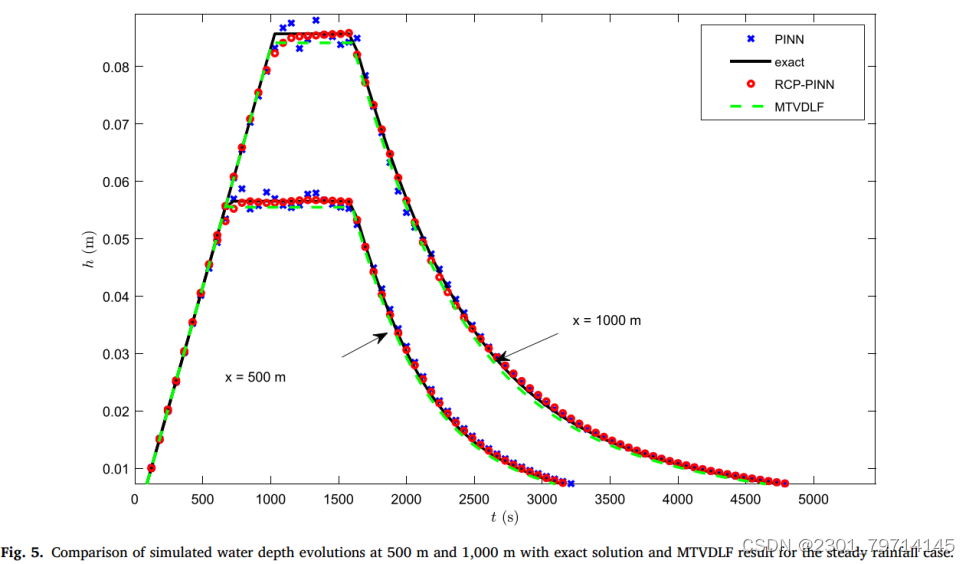
图5特别选取x = 500 m和x = 1000 m处的截面结果进行对比。结果表明：

RCP-PINN更精确地逼近了精确解，在抑制伪振荡方面表现更好。MTVDLF结果的峰值略低于精确解，但稳定性优于PINN和RCP-PINN。

为了保证实验的可靠性，检验算法的稳定性，文章重复进行了10次独立实验，PINN和RCP-PINN的相对误差均值分别为0.022和0.016，误差降低了25.5%，进一步验证了算法的有效性：

不稳定降雨情况

样例设置与上述稳流情况相同，非稳态降雨速率I (cm/h)满足下式:

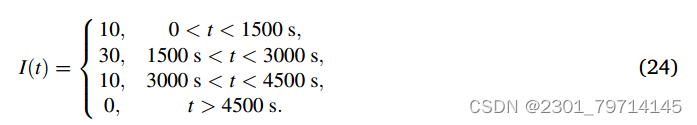
参考解采用三次样条插值(CSMOC)特征法得到，CSMOC的空间步长Δx为100 m，时间步长Δt为150 s, MTVDLF的Δx = 10 m， Δt = 1 s。PINN和RCP-PINN在时域和下游边界处得到的水深结果分别如图6和图7所示：

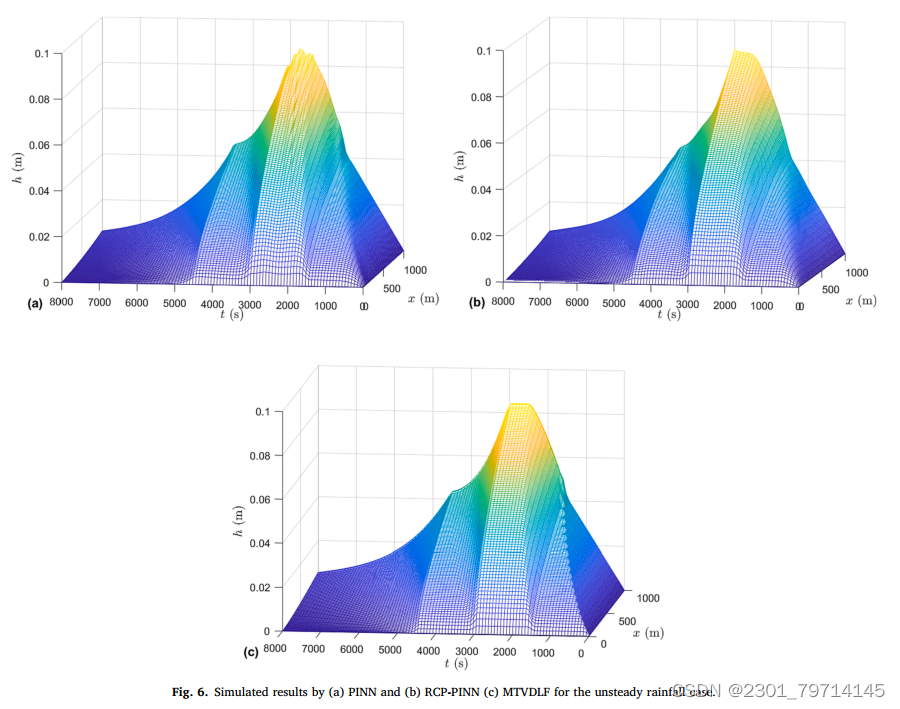
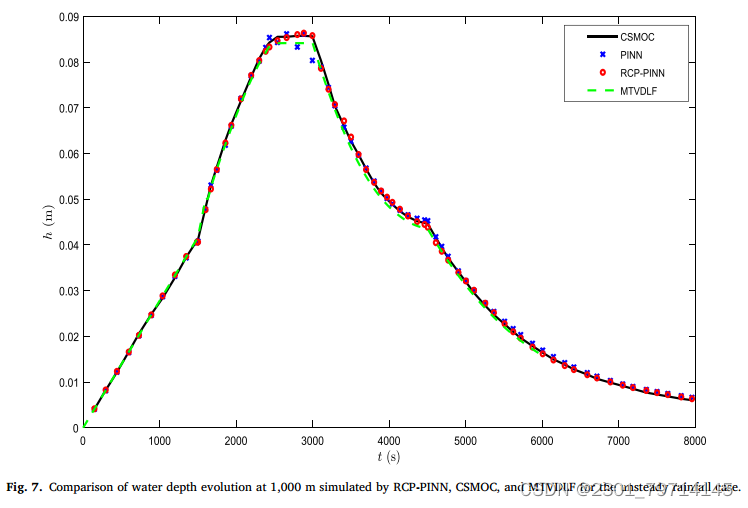
总体上与参考解和MTVDLF解吻合较好，但在水深趋于最大的位置，PINN的耗散误差较大(图7)，通过RCP-PINN中配置点的重新分配，耗散误差得到了很大的改善。MTVDLF溶液的峰值也略低于参考溶液;

从数值误差的角度，将下游端PINN和RCP-PINN的解与参考解进行了比较。与CSMOC相比，PINN和RCP-PINN的计算误差分别为0.016和0.012。这一结果表明准确率提高了28.7%。在稳定性方面，两种方法的标准差分别为0.0052和0.0031，表明RCP-PINN有效避免了较大偶然误差的发生。

图8显示了RCP-PINN和PINN的搭配点选择，其中点被重新分配到梯度变化较大的位置。重新分配的并置点不一定只集中在这些位置：

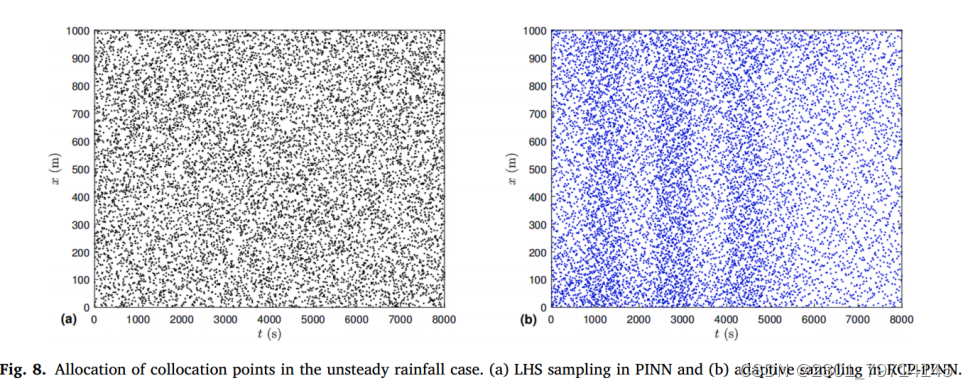
逆运动波问题

设置与前文相同，需要给出Manning系数的初始训练值，在迭代过程中逐渐接近真实值。假设真实值为0.02，初始训练值为1.0。观测数据取自10 × 10正交网格点。

以经典模拟退火(SA)算法为参考，假设观测数据由MTVDLF给出。SA的参数为:初始温度1.0，结束温度10-6，冷却系数0.9，最大迭代次数20，初始猜测值0.01，最佳代价初始化为无穷大。

表1为PINN、RCP-PINN和SA+MTVDLF对nm的预测结果。实验独立重复了10次，以比较这些算法的稳定性和准确性。在相同训练周期和计算代价的情况下，RCP-PINN在重复训练时的预测结果比PINN更接近真实值，也更稳定。在计算成本方面，SA+MTVDLF大约是PINN和RCP-PINN的50倍：

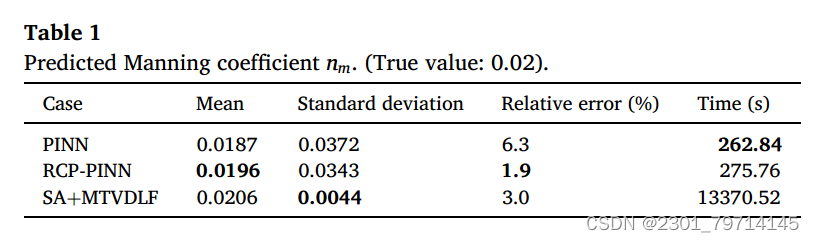
选择观测点如图10所示：

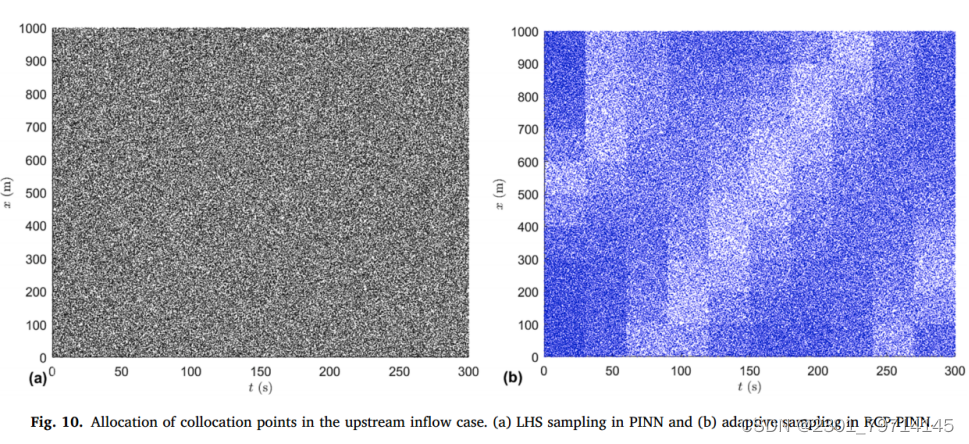
两种方法在20000个epoch下的训练损失过程如图11所示。可以看出，RCP-PINN的损失收敛到一个较小的值，而PINN的损失波动要大得多。这意味着在固定历元的条件下，与PCR-PINN相比，PINN更有可能停止在一个相对较差的解，训练过程可能不会停止在预期的收敛位置：

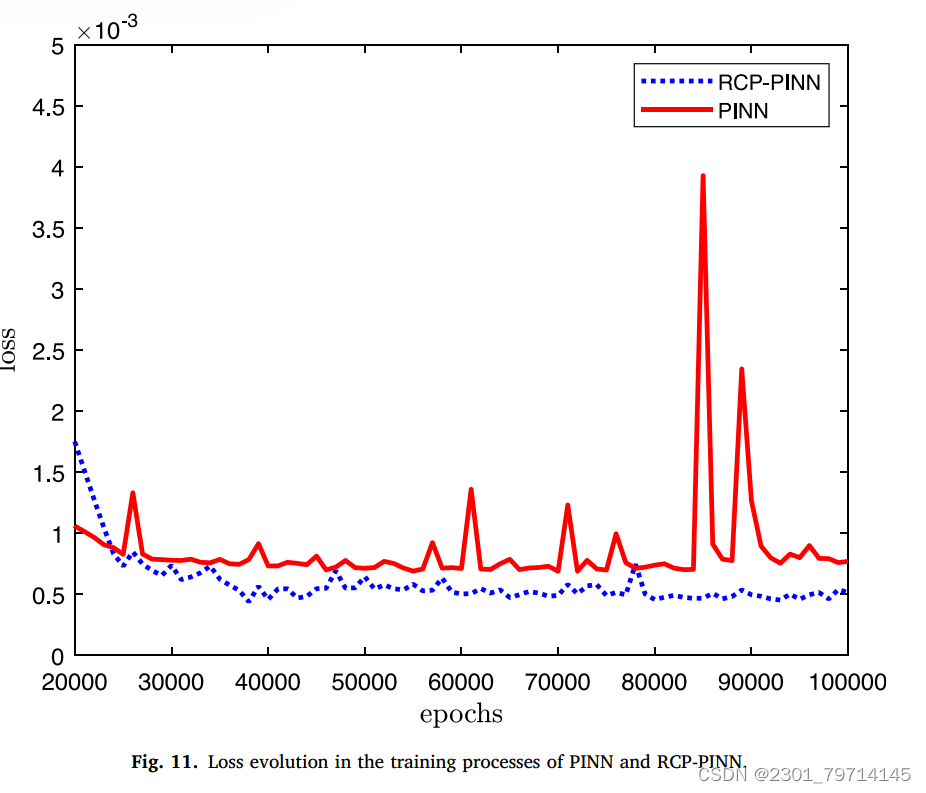
Fluent实例：分流管道中的流动分析

几何建模

在XY平面上绘制几何图形，单位调整成为mm，绘制如下图形，具体尺寸见图中：

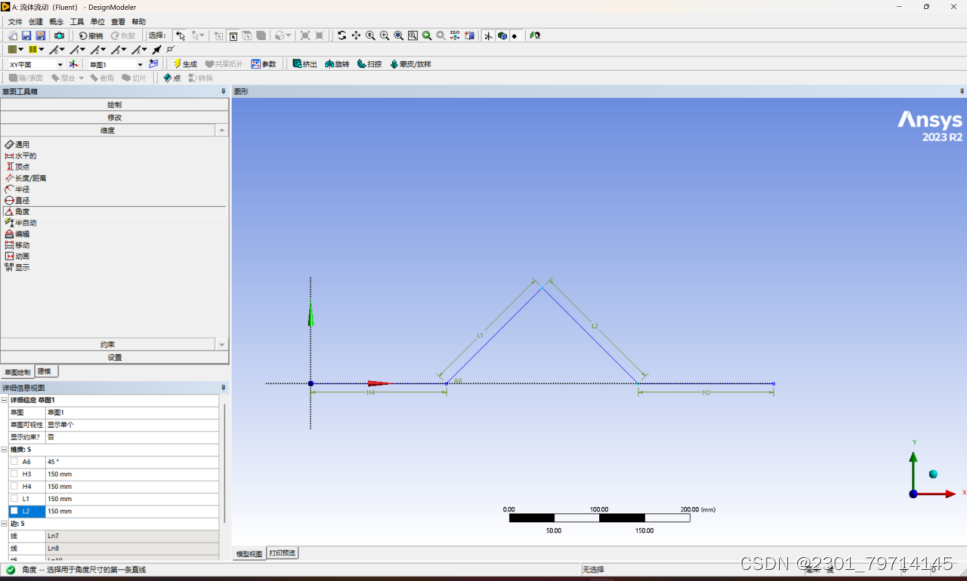
采用圆角命令，采用圆角的半径为150mm，将拐角处进行圆角操作，再采用50mm的圆角命令，将三角形顶点进行圆角操作：

在YZ平面中新建草图，绘制一个原点的5mm直径圆，右键选择两个草图，选择总是显示的命令，采用扫掠命令，圆为轮廓，线为路径，生成管道：

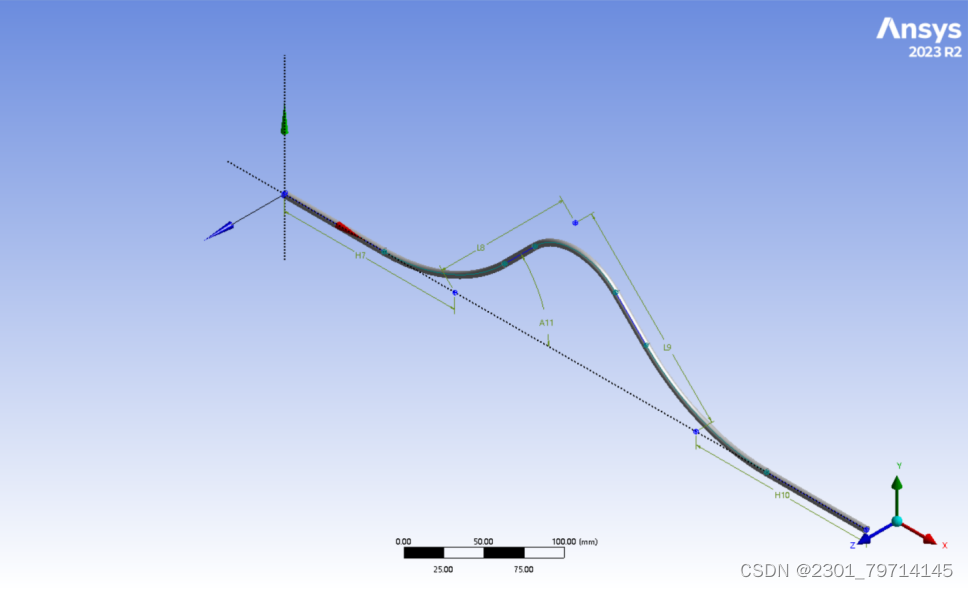
在创建菜单中采用模式命令，方向采用圆形，轴选用X轴，将会环绕X轴创作，拷贝数为4，生成如下：

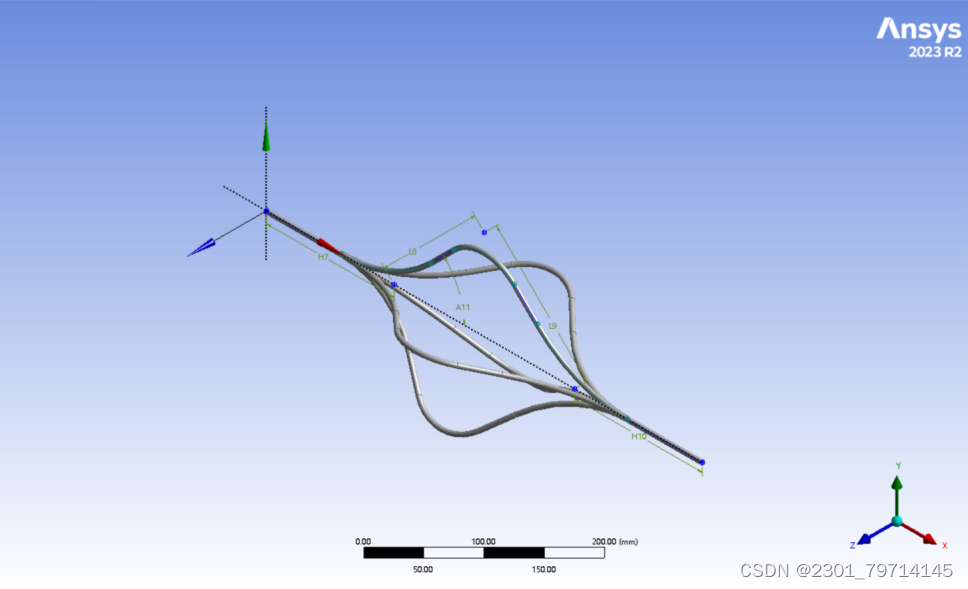
网格划分

生成默认网格，可以看出各网格的单元质量都趋近与0.9，故可以考虑该套网格，做完边界条件命名，更新网格后进入Fluent求解器中：

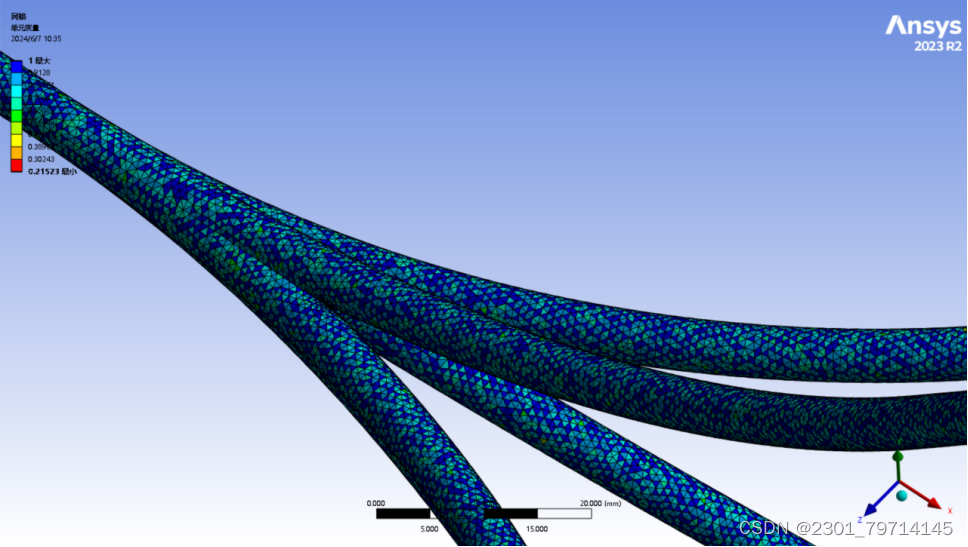
求解器设置

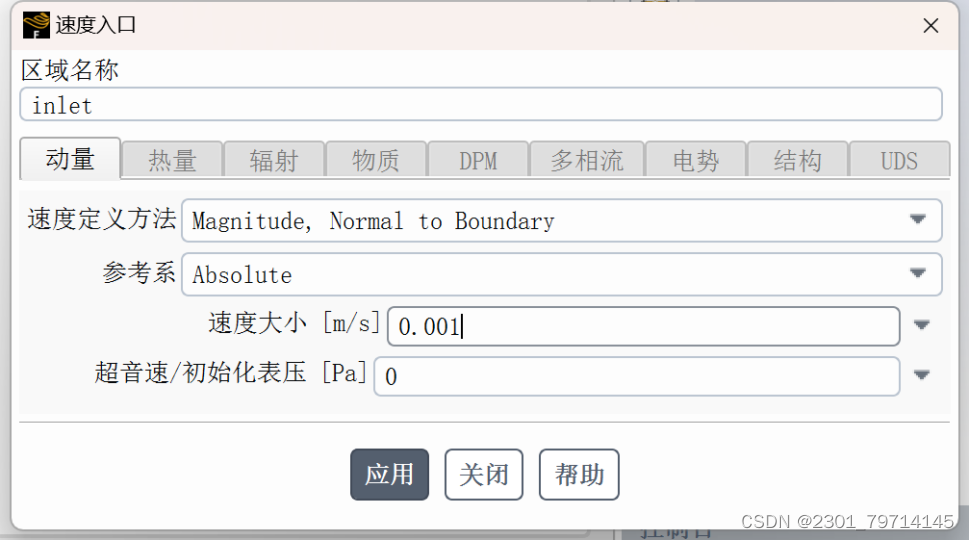
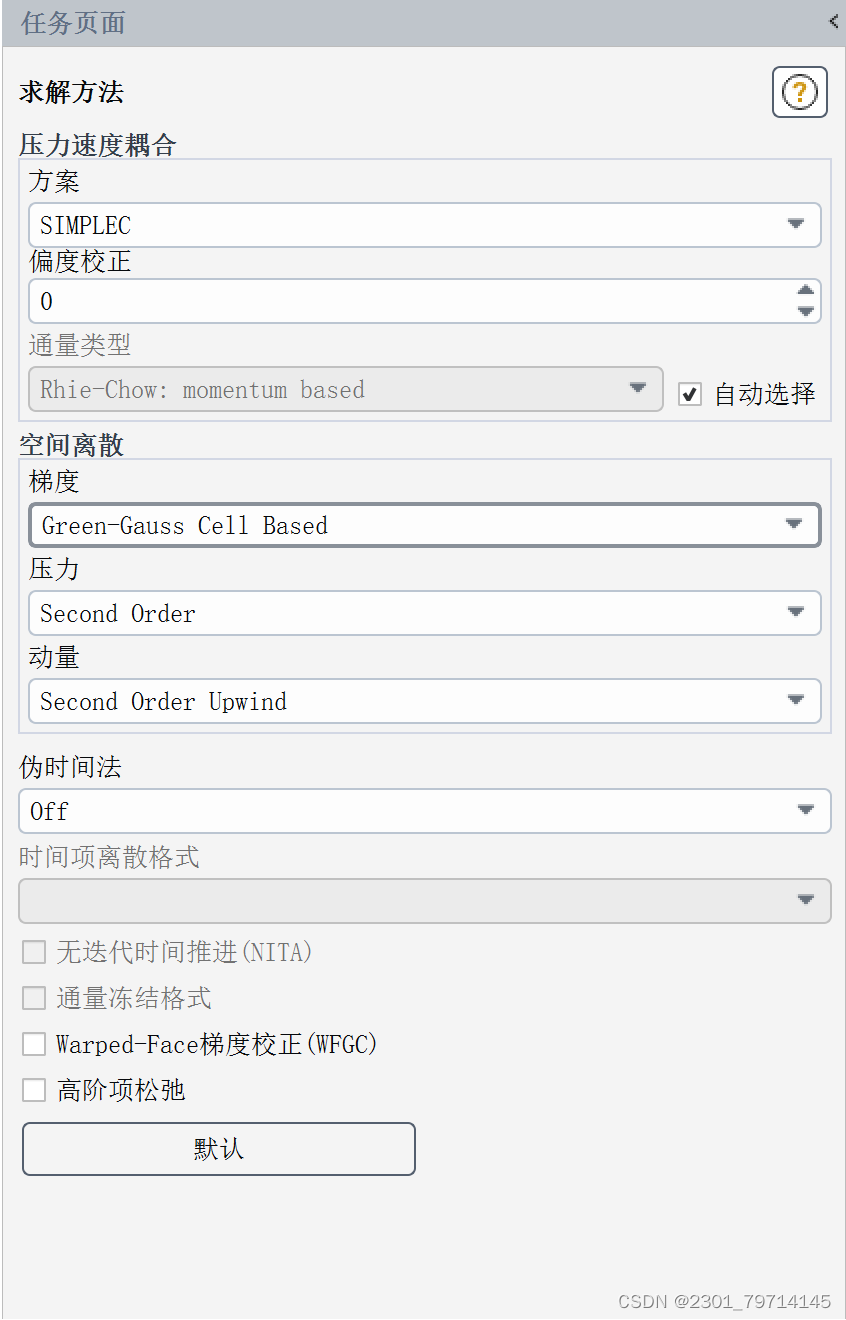
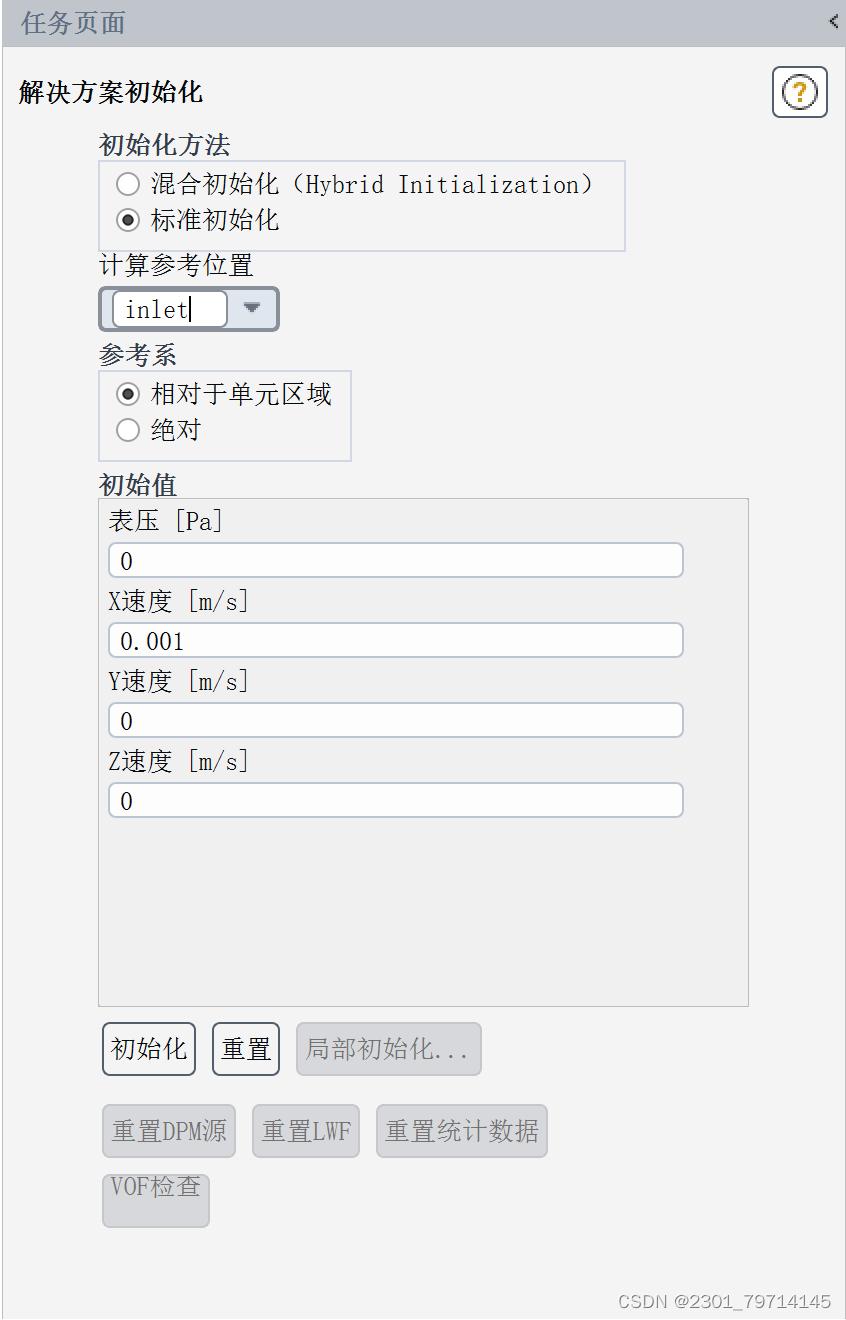
采用层流模型进行求解，添加流体材料为水，边界条件设置如下，若没特别指出，保持默认选择，残差监控设置为1e-6，迭代次数为1000，求解器方法、初始化条件如下所示：

结果展示

残差收敛：

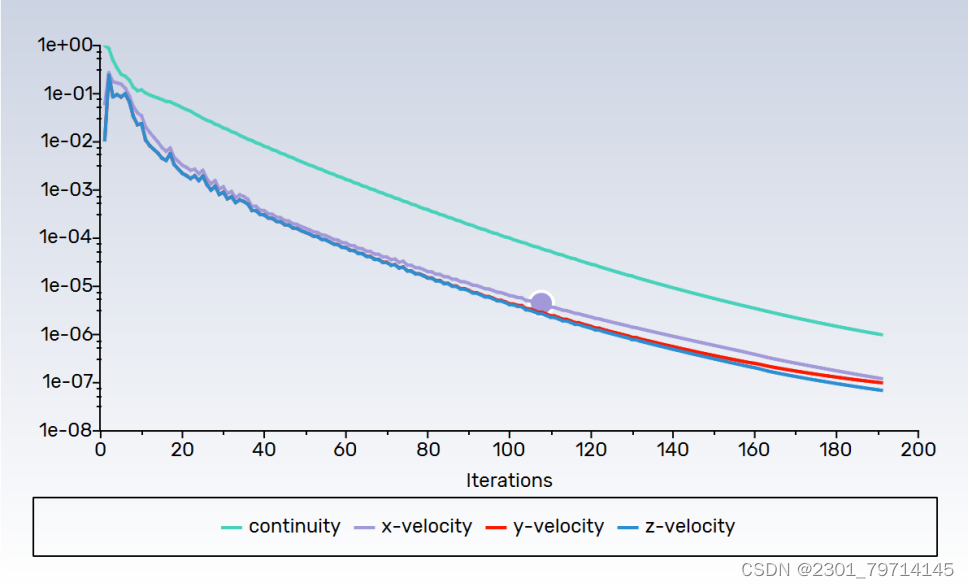
速度云图：

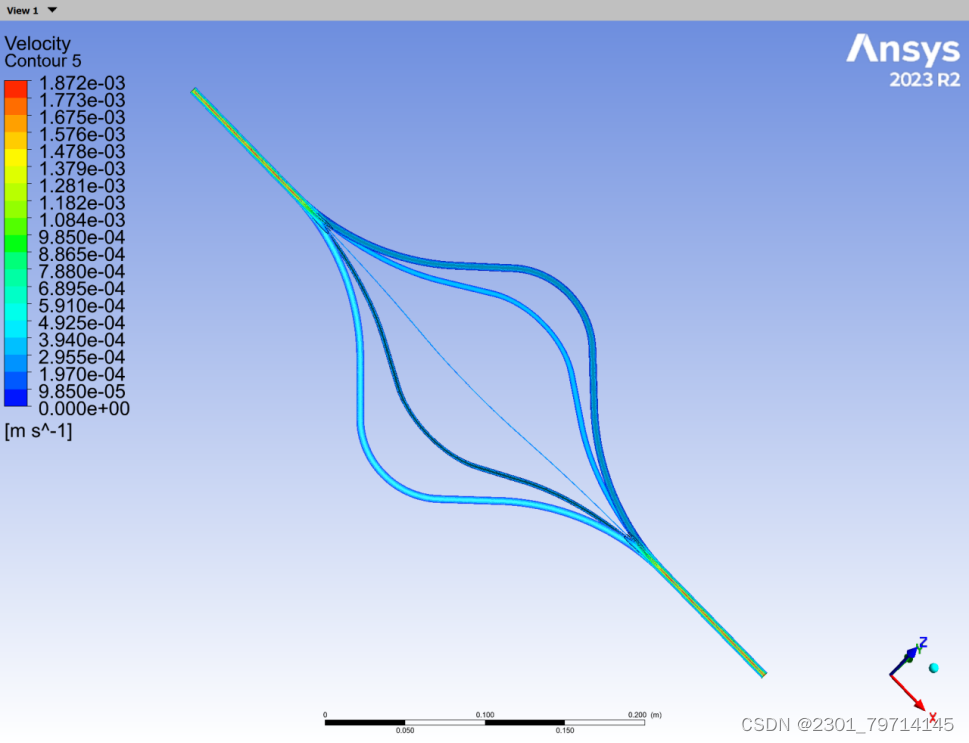
流线图：

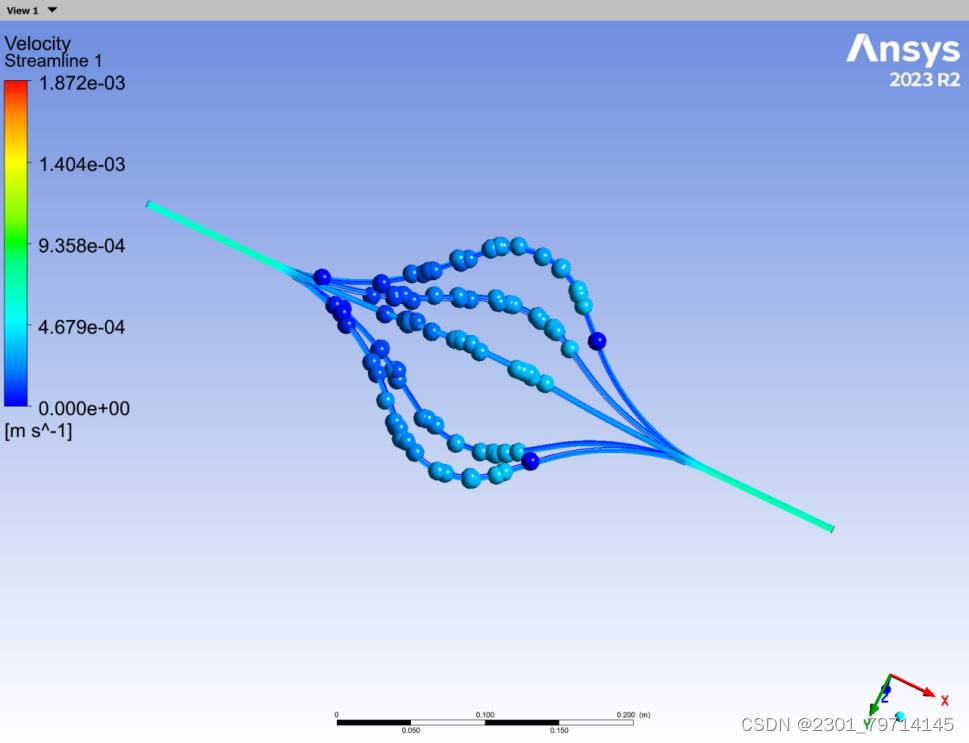
压力云图：

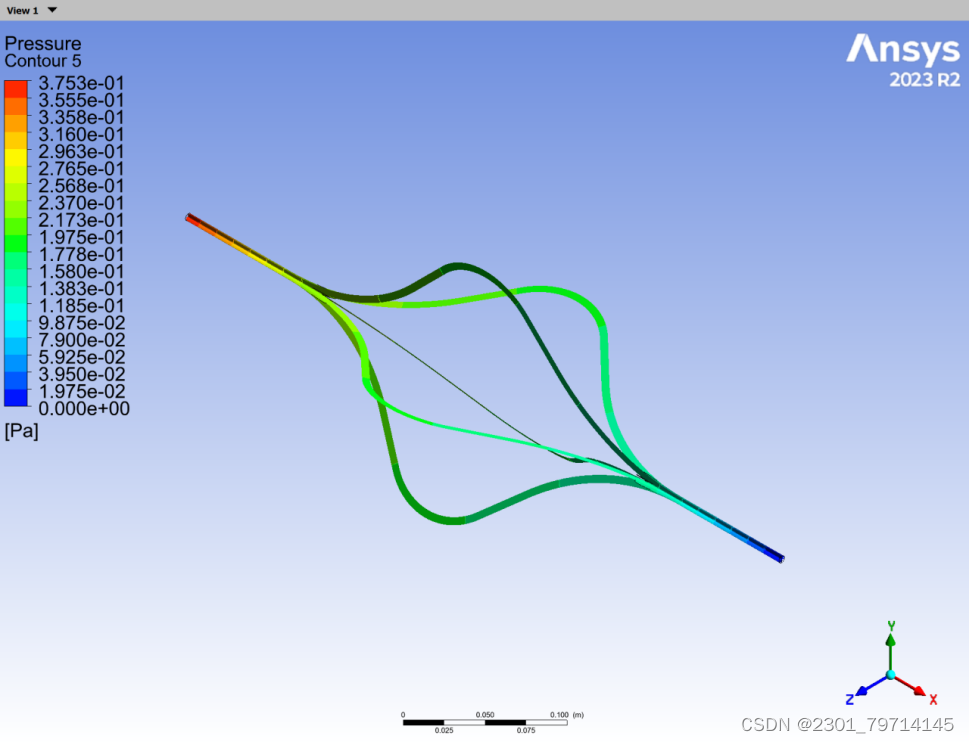
理论学习部分

总结

本周学习了新型PINN，关于重分配点的相关理论知识我还没有进行学习，故阅读中所遇到相关理论时显得有些无助，若出现讲不明白的地方麻烦进行指正，关于有限体积法相关知识已经基本叙述完毕，为了能更好的掌握Fluent这款软件，以后将会针对其中出现的算法进行学习。