近似消息传递(Approximate Message Passing)算法简介

近似消息传递(Approximate Message Passing)算法简介

1 前言

近似消息传递(Approximate Message Passing, AMP)算法是基于消息传递算法，也叫和-积算法(Sum-Product Algorithm, SPA)，还被称为置信传播(Belief Propagation, BP)算法，经过一系列假设与简化得来，这其中包括了中心极限定理(Central Limit Theory, CLT)和泰勒级数(Taylor Series)展开等[@zou_concise_2022]。

2 基础知识

这一节简单介绍基础知识，包括SPA、CLT、高斯分布乘以高斯分布、泰勒级数以及后验概率密度函数的偏导数求法的结果。

2.1 和-积算法(Sum-Product Algorithm, SPA)

消息传递算法是基于因子图(factor graph)的节点(node)之间的消息沿边(edge)相互传递而得名。

我们假设一个线性估计模型：

y

=

H

x

+

w

(

1

)

\mathbf{y = Hx + w} \quad(1)

y=Hx+w(1)
其中，

y

∈

C

M

\mathbf{y} \in \mathbb{C}^M

y∈CM是已知的观测数据(observed data)，

H

∈

C

M

×

N

\mathbf{H} \in \mathbb{C}^{M imes N}

H∈CM×N是已知的观测矩阵，

x

∈

C

N

\mathbf{x}\in \mathbb{C}^N

x∈CN是待估计的信号，并且知道先验分布为

p

(

x

)

p(\mathbf{x})

p(x)，

w

∈

C

M

\mathbf{w} \in \mathbb{C}^M

w∈CM是复高斯白噪声，即

w

∼

C

N

(

w

;

0

,

σ

2

I

)

\mathbf{w} \sim \mathcal{CN}(\mathbf{w};\mathbf{0},\sigma^2 \mathbf{I})

w∼CN(w;0,σ2I)。

根据公式(1)存在一个全局概率密度分布(global probability density distribution,PDF)

p

(

y

,

x

∣

H

)

p(\mathbf{y,x|H})

p(y,x∣H)，为了简单起见，我们省略

H

\mathbf{H}

H，写为

p

(

y

,

x

)

p(\mathbf{y,x})

p(y,x)。我们假设

y

\mathbf{y}

y和

x

\mathbf{x}

x的各自的元素都是分别各自独立同分布的。那么我们可以将全局PDF进行分解：

p

(

y

,

x

)

=

p

(

y

∣

x

)

p

(

x

)

(

2

)

=

∏

a

M

p

(

y

a

∣

x

)

∏

i

N

p

(

x

i

)

(

3

)

=

∏

a

f

a

(

x

)

(

4

)

\begin{aligned} p(\mathbf{y,x}) & = p(\mathbf{y|x})p(\mathbf{x}) \quad(2) \ & = \prod_a^M p(y_a |\mathbf{x}) \prod_i^N p(x_i) \quad(3)\ & = \prod_a f_a(\mathbf{x}) \quad(4) \end{aligned}

p(y,x)​=p(y∣x)p(x)(2)=a∏M​p(ya​∣x)i∏N​p(xi​)(3)=a∏​fa​(x)(4)​ 公式(2)是条件概率公式，公式(3)是根据独立假设而得来，公式(4)是因子形式分解，中的

x

\mathbf{x}

x是与该因子相连的全部变量，不是待估计的信号

x

∈

C

N

\mathbf{x}\in \mathbb{C}^N

x∈CN。

从变量节点

x

i

x_i

xi​传递到因子节点

f

a

(

x

)

f_a(\mathbf{x})

fa​(x)的消息为：

μ

i

→

a

(

x

i

)

∝

∏

b

≠

a

μ

i

←

b

(

x

i

)

(

5

)

\mu_{i \rightarrow a}(x_i) \propto \prod_{b
eq a} \mu_{i \leftarrow b}(x_i) \quad(5)

μi→a​(xi​)∝b=a∏​μi←b​(xi​)(5)

从因子节点

f

a

(

x

)

f_a(\mathbf{x})

fa​(x)传递到变量节点

x

i

x_i

xi​的消息为：

μ

i

←

a

(

x

i

)

∝

∫

x

\

i

f

a

(

x

)

∏

j

≠

i

μ

j

→

a

(

x

j

)

d

x

\

i

(

6

)

\mu_{i \leftarrow a}(x_i) \propto \int_{\mathbf{x}_{\backslash i}} f_a(\mathbf{x}) \prod_{j
eq i}\mu_{j \rightarrow a}(x_j) \mathbf{d} \mathbf{x}_{\backslash i} \quad(6)

μi←a​(xi​)∝∫x\i​​fa​(x)j=i∏​μj→a​(xj​)dx\i​(6)

j

≠

i

j
eq i

j=i和

b

≠

a

b
eq a

b=a的原因是避免传递自身的消息，即传递外信息，从而不会出现自己不断置信自己的情况。消息的本质是PDF，由于这里未进行归一化，所以使用正比于

∝

\propto

∝。

对于我们处理的模型，

M

×

N

M imes N

M×N的因子图为：

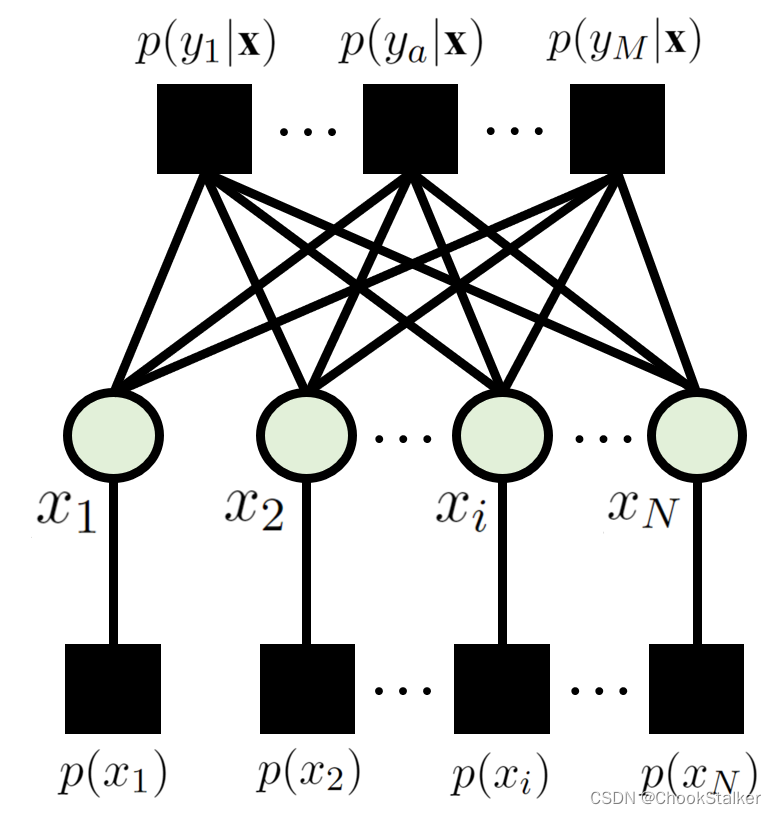
这张图省略了观测变量

y

\mathbf{y}

y，可以画出来，再用斜线涂黑，代表观测。整张图只有两种不同的节点，并且相同类型的节点不会连接，分别是变量节点(variable node)和因子节点(factor node)，又叫校验节点。消息在两类不同的节点之间相互传递。

那么对于上图来说，公式(5)和(6)可以分别写为：

μ

i

→

a

(

x

i

)

∝

p

(

x

i

)

∏

b

≠

a

μ

i

←

b

(

x

i

)

(

7

)

μ

i

←

a

(

x

i

)

∝

∫

x

\

i

p

(

y

a

∣

x

)

∏

j

≠

i

N

μ

j

→

a

(

x

j

)

d

x

\

i

(

8

)

\begin{aligned} \mu_{i \rightarrow a}(x_i) & \propto p(x_i) \prod_{b
eq a} \mu_{i \leftarrow b}(x_i) \quad(7) \ \mu_{i \leftarrow a}(x_i) & \propto \int_{\mathbf{x}_{\backslash i}} p(y_a|\mathbf{x}) \prod_{j
eq i}^N \mu_{j \rightarrow a}(x_j) \mathbf{d} \mathbf{x}_{\backslash i} \quad(8) \end{aligned}

μi→a​(xi​)μi←a​(xi​)​∝p(xi​)b=a∏​μi←b​(xi​)(7)∝∫x\i​​p(ya​∣x)j=i∏N​μj→a​(xj​)dx\i​(8)​
注意公式(5)和(6)是最一般的形式，即公式(4)，而公式(7)和(8)是针对公式(3)得来。可以看出来公式(7)和(8)只是变量节点

x

i

x_i

xi​和因子节点

p

(

y

a

∣

x

)

p(y_a|\mathbf{x})

p(ya​∣x)之间在进行消息传递，而没有

x

i

x_i

xi​与

p

(

x

i

)

p(x_i)

p(xi​)之间的传递。这是因为

p

(

x

i

)

p(x_i)

p(xi​)是边缘节点，只与

x

i

x_i

xi​相连，只能传递给

x

i

x_i

xi​消息

p

(

x

i

)

p(x_i)

p(xi​)，所以不需要更新。或者说，因为传递的是外信息，

p

(

x

i

)

p(x_i)

p(xi​)就算被更新了，也是传递最原始的先验知识

p

(

x

i

)

p(x_i)

p(xi​)。

由于这里的因子图不是可以得到精确解的树状结构，而是环状结构，消息会在两种节点间进行迭代，得到近似解。所以，我们把公式(7)和(8)重写为：

μ

i

→

a

t

+

1

(

x

i

)

∝

p

(

x

i

)

∏

b

≠

a

μ

i

←

b

(

x

i

)

(

9

)

μ

i

←

a

t

(

x

i

)

∝

∫

x

\

i

p

(

y

a

∣

x

)

∏

j

≠

i

N

μ

j

→

a

(

x

j

)

d

x

\

i

(

10

)

\begin{aligned} \mu_{i \rightarrow a}^{t+1}(x_i) & \propto p(x_i) \prod_{b
eq a} \mu_{i \leftarrow b}(x_i) \quad(9) \ \mu_{i \leftarrow a}^{t}(x_i) & \propto \int_{\mathbf{x}_{\backslash i}} p(y_a|\mathbf{x}) \prod_{j
eq i}^N \mu_{j \rightarrow a}(x_j) \mathbf{d} \mathbf{x}_{\backslash i} \quad(10) \end{aligned}

μi→at+1​(xi​)μi←at​(xi​)​∝p(xi​)b=a∏​μi←b​(xi​)(9)∝∫x\i​​p(ya​∣x)j=i∏N​μj→a​(xj​)dx\i​(10)​ 其中

t

t

t是第

t

t

t次迭代。

对于我们的需要的后验知识，可以利用下式求出后验分布：

p

(

x

i

t

)

∝

p

(

x

i

)

∏

a

=

1

M

μ

i

←

a

t

(

x

i

)

(

11

)

p(x_i^t) \propto p(x_i) \prod_{a=1}^{M} \mu_{i \leftarrow a }^t (x_i) \quad(11)

p(xit​)∝p(xi​)a=1∏M​μi←at​(xi​)(11)
即把所有与

x

i

x_i

xi​相连的因子节点传递给它的消息进行合并，这被称为因子图的边缘分布，但并不是一般的概率分布的边缘分布(marginal
distribution)，它实际上是后验分布

p

(

x

i

∣

y

)

p(x_i|\mathbf{y})

p(xi​∣y)。

至此，我们完成了简要讨论SPA。

2.2 中心极限定理(Central Limit Theory, CLT)

我们这里考虑最简单的独立同分布(independent identical distribution, i.i.d.)的形式，也叫Lindeberg-Feller中心极限定理。

定理 1 (独立同分布中心极限定理).
假设

{

X

n

}

n

=

1

N

\{X_n\}^N_{n=1}

{Xn​}n=1N​的

N

N

N个样本是i.i.d.的，有

E

(

X

n

)

=

m

\mathbb{E}(X_n) = m

E(Xn​)=m且

V

a

r

(

X

n

)

=

σ

2

>

0

{\rm Var}(X_n) = \sigma^2 > 0

Var(Xn​)=σ2>0。当

N

N

N足够大时，

X

ˉ

n

=

1

N

∑

n

=

1

N

X

n

\bar{X}_n = \frac{1}{N}\sum_{n=1}^{N}X_n

Xˉn​=N1​∑n=1N​Xn​近似服从正态分布

N

(

m

,

σ

2

N

)

\mathcal{N}(m, \frac{\sigma^2}{N})

N(m,Nσ2​)。

我们这里将正态分布重写为标准正态分布，即

X

ˉ

n

−

m

σ

/

N

∼

N

(

0

,

1

)

\frac{\bar{X}_n – m}{\sigma / \sqrt{N} } \sim \mathcal{N}(0, 1)

σ/N

​Xˉn​−m​∼N(0,1)。同样的，在复数域下，可以写为

X

ˉ

n

−

m

σ

/

N

∼

C

N

(

0

,

1

)

\frac{\bar{X}_n – m}{\sigma / \sqrt{N} } \sim \mathcal{CN}(0, 1)

σ/N

​Xˉn​−m​∼CN(0,1)

2.3 高斯分布乘高斯分布

接下来介绍高斯分布乘高斯分布的引理：

定理 2 (Gaussian reproduction lemma).
对于两个高斯分布，

N

(

x

;

a

,

A

)

\mathcal{N}(x;a,A)

N(x;a,A)和

N

(

x

;

b

,

B

)

\mathcal{N}(x;b,B)

N(x;b,B)，它们的乘积为：

N

(

x

;

a

,

A

)

N

(

x

;

b

,

B

)

=

N

(

x

;

c

,

C

)

N

(

0

;

a

−

b

,

A

+

B

)

∝

N

(

x

;

c

,

C

)

(

12

)

\mathcal{N}(x;a,A)\mathcal{N}(x;b,B) = \mathcal{N}(x;c,C)\mathcal{N}(0;a-b,A+B) \propto \mathcal{N}(x;c,C) \quad(12)

N(x;a,A)N(x;b,B)=N(x;c,C)N(0;a−b,A+B)∝N(x;c,C)(12)其中

1

C

=

1

A

+

1

B

\frac{1}{C} = \frac{1}{A} + \frac{1}{B}

C1​=A1​+B1​,

c

C

=

a

A

+

b

B

\frac{c}{C} = \frac{a}{A} + \frac{b}{B}

Cc​=Aa​+Bb​。

这里的证明很简单，简单的想办法把两个高斯分布的乘积拼凑高斯分布的形式即可，可以很显式地得出均值和方差，可以将等式两边除以

N

(

0

;

a

−

b

,

A

+

B

)

\mathcal{N}(0;a-b,A+B)

N(0;a−b,A+B)以归一化，得到真正的PDF。同样的，给出复数域的情况：

C

N

(

x

;

a

,

A

)

C

N

(

x

;

b

,

B

)

=

C

N

(

x

;

c

,

C

)

C

N

(

0

;

a

−

b

,

A

+

B

)

∝

C

N

(

x

;

c

,

C

)

(

13

)

\mathcal{CN}(x;a,A)\mathcal{CN}(x;b,B) = \mathcal{CN}(x;c,C)\mathcal{CN}(0;a-b,A+B) \propto \mathcal{CN}(x;c,C)\quad(13)

CN(x;a,A)CN(x;b,B)=CN(x;c,C)CN(0;a−b,A+B)∝CN(x;c,C)(13)至此，我们完成了基础知识的简单介绍。

2.4 一阶泰勒级数展开

对于一个两变量的函数

f

(

x

,

y

)

f(x,y)

f(x,y)，并假设其Lipschitz连续，我们一阶泰勒级数展开有：

f

(

x

+

Δ

x

,

y

+

Δ

y

)

≈

f

(

x

,

y

)

+

Δ

x

f

x

′

(

x

,

y

)

+

Δ

y

f

y

′

(

x

,

y

)

(

14

)

f(x+\Delta x ,y+\Delta y ) \approx f(x,y) + \Delta x f’_x(x,y)+ \Delta y f’_y(x,y)\quad(14)

f(x+Δx,y+Δy)≈f(x,y)+Δxfx′​(x,y)+Δyfy′​(x,y)(14)其中，

f

x

′

f’_x

fx′​和

f

y

′

f’_y

fy′​分别代表了对

x

x

x和

y

y

y分别求偏导。

2.5 后验概率密度函数的偏导数求法

对于一个任意有界非负的函数

f

(

x

)

f(x)

f(x)（其实是加权），并定义一个分布

P

(

x

)

=

f

(

x

)

C

N

(

x

;

m

,

v

)

∫

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

\mathcal{P}(x) = \frac{f(x)\mathcal{CN}(x;m,v)}{\int f(x)\mathcal{CN}(x;m,v) {\rm d}x}

P(x)=∫f(x)CN(x;m,v)dxf(x)CN(x;m,v)​。其均值和方差表示为

E

(

x

)

=

∫

x

P

(

x

)

d

x

\mathbb{E}(x) = \int x \mathcal{P}(x) {\rm d}x

E(x)=∫xP(x)dx和

V

a

r

(

x

)

=

∫

[

x

−

E

(

x

)

]

2

P

(

x

)

d

x

{\rm Var}(x) = \int [x – \mathbb{E}(x)]^2 \mathcal{P}(x) {\rm d}x

Var(x)=∫[x−E(x)]2P(x)dx。我们有：

∂

∫

x

P

(

x

)

d

x

∂

m

=

∫

x

x

−

m

v

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

⋅

∫

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

[

∫

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

]

2

−

∫

x

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

⋅

∫

x

−

m

v

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

[

∫

f

(

x

)

C

N

(

x

;

m

,

v

)

d

x

]

2

=

V

a

r

(

x

)

v

(

15

)

\begin{split} \frac{\partial \int x \mathcal{P}(x) {\rm d}x }{\partial m} & = \frac{\int x \frac{x-m}{v} f(x) \mathcal{CN}(x;m,v){\rm d}x \cdot \int f(x) \mathcal{CN}(x;m,v){\rm d}x }{[\int f(x)\mathcal{CN}(x;m,v){\rm d}x ]^2} \ & \quad – \frac{\int x f(x) \mathcal{CN}(x;m,v){\rm d}x \cdot \int \frac{x-m}{v} f(x) \mathcal{CN}(x;m,v){\rm d}x }{[\int f(x)\mathcal{CN}(x;m,v){\rm d}x ]^2} \ & = \frac{{\rm Var}(x)}{v} \end{split}\quad(15)

∂m∂∫xP(x)dx​​=[∫f(x)CN(x;m,v)dx]2∫xvx−m​f(x)CN(x;m,v)dx⋅∫f(x)CN(x;m,v)dx​−[∫f(x)CN(x;m,v)dx]2∫xf(x)CN(x;m,v)dx⋅∫vx−m​f(x)CN(x;m,v)dx​=vVar(x)​​(15)

3 AMP推导

我们回到SPA的模型以及公式(9)和(10)，开始对它们进行简化。

3.1 从因子节点传递到变量节点的消息

对于公式(10)中的

p

(

y

a

∣

x

)

p(y_a|\mathbf{x})

p(ya​∣x)而言，我们这里不再省略

H

\mathbf{H}

H，并用

H

a

∼

\mathbf{H}_{a\sim}

Ha∼​表示其第

a

a

a行：

p

(

y

a

∣

H

,

x

)

=

p

w

a

(

y

a

−

H

a

∼

x

)

=

C

N

(

y

a

;

H

a

∼

x

,

σ

2

)

=

C

N

(

w

a

=

y

a

−

H

a

∼

x

;

0

,

σ

2

)

(

16

)

=

1

π

σ

2

exp

⁡

(

−

∣

y

a

−

H

a

∼

x

∣

2

σ

2

)

\begin{split} p(y_a|\mathbf{H,x}) & = p_{w_a}(y_a – \mathbf{H}_{a\sim}\mathbf{x} ) \ & = \mathcal{CN}(y_a;\mathbf{H}_{a\sim}\mathbf{x} , \sigma^2 ) \ & = \mathcal{CN}(w_a = y_a – \mathbf{H}_{a\sim}\mathbf{x}; 0, \sigma^2 )\quad(16)\ & = \frac{1}{\pi \sigma^2}\exp( \frac{-|y_a – \mathbf{H}_{a\sim}\mathbf{x}|^2}{\sigma^2} ) \end{split}

p(ya​∣H,x)​=pwa​​(ya​−Ha∼​x)=CN(ya​;Ha∼​x,σ2)=CN(wa​=ya​−Ha∼​x;0,σ2)(16)=πσ21​exp(σ2−∣ya​−Ha∼​x∣2​)​
其中

p

w

a

(

⋅

)

p_{w_a}(\cdot)

pwa​​(⋅)代表是随机变量

w

a

w_a

wa​的PDF，

H

a

∼

x

\mathbf{H}_{a\sim}\mathbf{x}

Ha∼​x也可以被写作

∑

k

=

1

N

h

a

k

x

k

\sum_{k=1}^{N}h_{ak}x_k

∑k=1N​hak​xk​。

为了简化公式(10)，我们将其重写为：

μ

i

←

a

t

(

x

i

)

∝

∫

x

\

i

p

(

y

a

∣

H

a

∼

x

)

∏

j

≠

i

N

μ

j

→

a

t

(

x

j

)

d

x

\

i

∝

∫

x

\

i

∫

z

a

p

(

y

a

∣

z

a

)

δ

(

z

a

−

∑

k

=

1

N

h

a

k

x

k

)

d

z

a

∏

j

≠

i

N

μ

j

→

a

t

(

x

j

)

d

x

\

i

∝

∫

z

a

p

(

y

a

∣

z

a

)

E

{

δ

(

z

a

−

∑

j

≠

i

N

h

a

j

x

j

−

h

a

i

x

i

)

}

d

z

a

(

17

)

\begin{split} \mu_{i \leftarrow a}^{t}(x_i) & \propto \int_{\mathbf{x}_{\backslash i}} p(y_a|\mathbf{H}_{a\sim}\mathbf{x}) \prod_{j
eq i}^N \mu_{j \rightarrow a}^t(x_j) \mathbf{d} \mathbf{x}_{\backslash i} \ & \propto \int_{\mathbf{x}_{\backslash i}} \int_{z_a} p(y_a|z_a) \delta(z_a – \sum_{k=1}^{N}h_{ak}x_k) {\rm d}z_a \prod_{j
eq i}^N \mu_{j \rightarrow a}^t(x_j) \mathbf{d} \mathbf{x}_{\backslash i}\ & \propto \int_{z_a} p(y_a|z_a) \mathbb{E}\left\{\delta \left( z_a – \sum_{j
eq i}^{N}h_{aj}x_j – h_{ai}x_i \right) \right\} {\rm d}z_a \quad(17) \end{split}

μi←at​(xi​)​∝∫x\i​​p(ya​∣Ha∼​x)j=i∏N​μj→at​(xj​)dx\i​∝∫x\i​​∫za​​p(ya​∣za​)δ(za​−k=1∑N​hak​xk​)dza​j=i∏N​μj→at​(xj​)dx\i​∝∫za​​p(ya​∣za​)E⎩

⎨

⎧​δ

​za​−j=i∑N​haj​xj​−hai​xi​

​⎭

⎬

⎫​dza​(17)​
其中，期望是基于

∏

j

≠

i

N

μ

j

→

a

t

(

x

j

)

\prod_{j
eq i}^N \mu_{j \rightarrow a}^t(x_j)

∏j=iN​μj→at​(xj​)求的。我们定义了新的随机变量

z

a

=

H

a

∼

x

z_a = \mathbf{H}_{a\sim}\mathbf{x}

za​=Ha∼​x，以及与它相关的随机变量

ζ

i

←

a

t

\zeta_{i \leftarrow a}^{t}

ζi←at​。再定义根据

μ

j

→

a

t

(

x

j

)

\mu_{j \rightarrow a}^{t}(x_j)

μj→at​(xj​)与

x

j

x_j

xj​相关的

ξ

j

→

a

t

\xi_{j \rightarrow a}^{t}

ξj→at​。并且给出

ξ

j

→

a

t

\xi_{j \rightarrow a}^{t}

ξj→at​的均值和方差分别为

x

^

j

→

a

t

\hat{x}_{j \rightarrow a}^{t}

x^j→at​和

v

^

j

→

a

t

\hat{v}_{j \rightarrow a}^{t}

v^j→at​。由公式(17)，当

N

N

N趋近于无穷时，根据CLT，可以得到随机变量

ζ

i

←

a

t

\zeta_{i \leftarrow a}^{t}

ζi←at​收敛到高斯随机变量，其均值和方差为：

E

(

ζ

i

←

a

t

)

=

Z

i

←

a

t

+

h

a

i

x

i

,

V

a

r

(

ζ

i

←

a

t

)

=

V

i

←

a

t

(

18

)

\mathbb{E}(\zeta_{i \leftarrow a}^{t}) = Z^t_{i \leftarrow a}+h_{ai}x_i , \quad {\rm Var}(\zeta_{i \leftarrow a}^{t}) = V_{i \leftarrow a}^t\quad(18)

E(ζi←at​)=Zi←at​+hai​xi​,Var(ζi←at​)=Vi←at​(18)
其中

Z

i

←

a

t

=

∑

j

≠

i

h

a

j

x

^

j

→

a

t

,

V

i

←

a

t

=

∑

j

≠

i

∣

h

a

j

∣

2

v

^

j

→

a

t

(

19

)

Z^t_{i \leftarrow a} = \sum_{j
eq i} h_{aj}\hat{x}^t_{j \rightarrow a}, \quad V_{i \leftarrow a}^t = \sum_{j
eq i} |h_{aj}|^2 \hat{v}^t_{j \rightarrow a } \quad(19)

Zi←at​=j=i∑​haj​x^j→at​,Vi←at​=j=i∑​∣haj​∣2v^j→at​(19)
实际上公式(19)可以视为在

x

∼

i

\mathbf{x}_{\sim i}

x∼i​下对

y

a

y_a

ya​的估计。

基于这里的高斯假设，我们可以将公式(17)中的

E

{

δ

(

z

a

−

∑

j

≠

i

N

h

a

j

x

j

−

h

a

i

x

i

)

}

\mathbb{E}\{\delta ( z_a – \sum_{j
eq i}^{N}h_{aj}x_j – h_{ai}x_i )\}

E{δ(za​−∑j=iN​haj​xj​−hai​xi​)}替换为，

C

N

(

z

a

;

h

a

i

x

i

+

Z

i

←

a

t

,

V

i

←

a

t

)

\mathcal{CN}(z_a ; h_{ai}x_i + Z^t_{i \leftarrow a}, V_{i \leftarrow a}^t)

CN(za​;hai​xi​+Zi←at​,Vi←at​)，再根据高斯分布乘高斯分布的引理，

μ

i

←

a

t

(

x

i

)

\mu_{i \leftarrow a}^{t}(x_i)

μi←at​(xi​)被近似为：

μ

i

←

a

t

(

x

i

)

∝

∫

z

a

p

(

y

a

∣

z

a

)

C

N

(

z

a

;

h

a

i

x

i

+

Z

i

←

a

t

,

V

i

←

a

t

)

d

z

a

∝

∫

z

a

C

N

(

y

a

;

H

a

∼

x

,

σ

2

)

C

N

(

z

a

;

h

a

i

x

i

+

Z

i

←

a

t

,

V

i

←

a

t

)

d

z

a

∝

∫

z

a

C

N

(

z

a

;

y

a

,

σ

2

)

C

N

(

z

a

;

h

a

i

x

i

+

Z

i

←

a

t

,

V

i

←

a

t